Mock exam, WiSe 2018/19 (Sailer)
The examples in the text are based on Shakespeare's play Macbeth. The full text of the play is available on Projekt Gutenberg.
We will use J.K. Rowling's Harry Potter novels for the final exam this term.
Task 1: Ambiguity
Consider the following ambiguous sentences. For each of them, provide an unambiguous paraphrase for the possible readings.
(1) a. Duncan trusted Macbeth because he was a thane.
Check your answer
Reading 1: he refers to Macbeth. Paraphrase: Duncan trusted Macbeth because Macbeth was a thane.
Reading 2: he refers to Duncan. Paraphrase: Duncan trusted Macbeth because Duncan was a thane.
b. Every king trusts a thane.
Check your answer
Reading 1: every takes scope over a. Paraphrase: For every king there is at least one thane such that the king trusts that thane.
Reading 2: a takes scope over every. Paraphrase: There is one particular thane such that each king trusts this thane.
b. Macbeth and Macduff are married.
Check your answer
Reading 1: collective reading. Paraphrase: Macbeth and Macduff are married to each other
Reading 2: distributive reading. Paraphrase: Macbeth and Macduff are both married, but not to each other.
b. Macbeth killed a king with a dagger.
Check your answer
Reading 1: the PP with a dagger is a modifier of the verb kill Paraphrase: Macbeth used a dagger to kill a king.
Reading 2: the PP with a dagger is a modifier of the noun king. Paraphrase: Macbeth killed a king who had a dagger.
Task 2: Model and Interpretation
1. Define a universe that consists of Macbeth and Banquo.
Check your answer
U = { Macbeth, Banquo }
2. Define the interpretation of the names macbeth and banquo in an intuitively plausible way.
Check your answer
I(macbeth) = Macbeth,
I(banquo) = Banquo
3. Define the interpretation of the properties thane1, king1, and witch1 is such a way that Macbeth is a king, both are thanes and neither is a witch.
Check your answer
I(thane1) = {<Macbeth>, <Banquo>},
I(king1) = {<Macbeth>},
I(witch1) = {}
4. Define the interpretation of the 2-place relations mistrust2 and kill2 in such a way that Macbeth and Banquo mistrust each other and Macbeth kills Banquo.
Check your answer
I(mistrust2) = {<Macbeth, Banquo>, <Banquo, Mactbeth>},
I(kill2) = {<Macbeth,Banquo>}
Task 3: Formulae
Write down logical formulae that express the meaning of the following sentences.
1. Banquo is a thane.
Check your answer
thane1(banquo)
2. Macbeth is king and Macbeth mistrusts Banquo.
Check your answer
king1(macbeth) ∧ mistrust2(macbeth,banquo)
3. If Banquo is king then Macbeth does not kill Banquo.
Check your answer
king1(banquo) ⊃ ¬ kill2(macbeth,banquo)
Task 4: Interpreting formulae
Compute the interpretation of the following formulæ step by step.
1. mistrust2(macbeth,macbeth)
Check your answer
[[mistrust2(macbeth,macbeth)]] = 1
iff < [[macbeth]], [[macbeth]] > is in [[mistrust2]]
iff < I(macbeth), I(macbeth) > in I(mistrust2)
iff < Macbeth, Macbeth > in { <x,y> | x mistrusts y } = { <Macbeth, Banquo>, <Banquo, Macbeth> }
Since this is not the case, [[mistrust2(macbeth,macbeth)]] = 0.
2. ¬king(banquo)
Check your answer
[[¬ king1(banquo)]] = 1
iff [[king(banquo)]] = 0
iff < [[banquo]]> is not in [[king1]]
iff < I(banquo> is not in I(king1)
iff < Banquo > is not in { <x> | x is king } = { <Macbeth>}
Since this is the case, [[¬ king1(banquo)]] = 1
3. witch1(banquo) ⊃ king1(macbeth)
Check your answer
[[witch1(banquo) ⊃ king1(macbeth))]] = 1
iff [[witch1(banquo)]] = 0 or [[king1(macbeth) = 1
iff < [[banquo]] > is not in [[witch1]] or < [[macbeth]] > is in [[king1]]
iff < I(banquo) > is not in I(witch1) or < I(macbeth) > is in I(king1)
iff < Banquo > is not in { <x> | x is a witch} = { } or < Macbeth > is in { <x> | x is king} = { <Macbeth>}.
Since both are the case, [[witch1(banquo) ⊃ king1(macbeth))]] = 1.
Task 5: Variables
Provide a g-function that maps the variables x, y, and z to individuals from the universe and compute the interpretation of the following formula with respect to the model and your g.
(i) kill2(z,x)
Check your answer
Example solution (other values for g are equally possible).
g(x) = Macbeth,
g(y) = Banquo,
g(z) = Banquo.
With this variable assignment we can compute the truth value of the formula:
[[kill2(z,x)]]g = 1
iff < [[z]]g, [[x]]g > is in [[kill2]]g
iff < g(z), g(x) > is in I(kill2)
iff < Banquo, Macbeth > is in { <x,y> | x killed y} = { <Macbeth, Banquo> }.
Since this is not the case, [[kill2(z,x)]]g = 0.
Task 6: Quantifiers
Provide logical formulae that expresse the meaning of the following sentences. Are the formulae true in your model (not in the entire play)? Give a short reason (you don’t need to compute the truth value).
1. Banquo was killed by a king.
Check your answer
∃x (king(x) : kill(x, banquo))
The formula is true in my model, because there is only one king, Macbeth, and Macbeth killed Banquo.
(Note: The English sentence is in passive, but this has no effect on the logical form.)
2. Macbeth mistrusts every witch.
Check your answer
∀x (witch(x) : mistrust(macbeth, x))
The formula is true in my model, because there are no witches in my model. Therefore, the formula with the universal quantifier is trivially true.
Task 7: Analysis: Lexicon
Provide the lexical entries for the words in the sentence Banquo mistrusted Macbeth. Use the features PHON, HEAD, SUBJ, SPR, COMPS, DR, PARTS, and EX-CONT.
Check your answer
| Banquo | mistrusted | Macbeth | |
| PHON | < Banquo > | < mistrusted > | < Macbeth > |
| HEAD | noun | verb | noun |
| SUBJ | < > | < NP[DR [a]] > | < > |
| SPR | < > | < > | < > |
| COMPS | < > | < NP[DR [b]] > | < > |
| DR | [x] | [c]mistrust2 | [y] |
| EX-C | ?? | ?? | ?? |
| PARTS | < [x]banquo > | < [c]mistrust2, [c]([a],[b]) > | < [y]macbeth > |
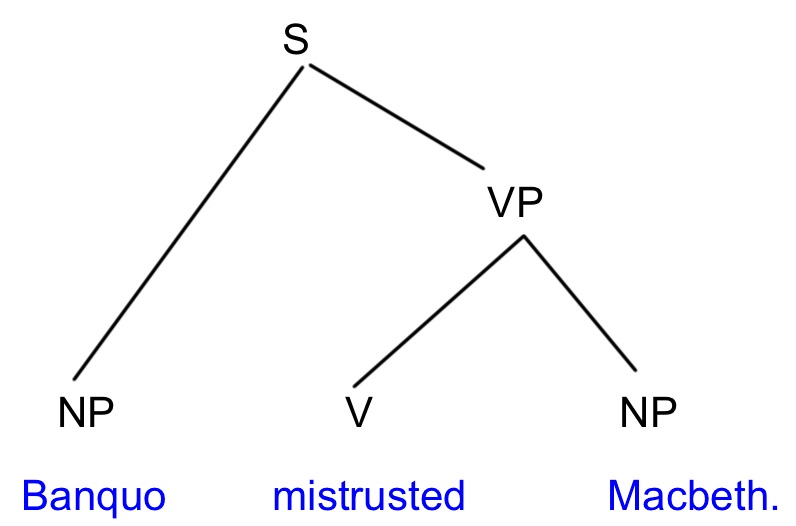
Task 8: Analysis: Syntactic structure and semantic combinatorics
Using the lexical entries from Task 7, provide the syntactic structure of the sentence Banquo mistrusted Macbeth. Indicate all the values for all features at each node in the tree.
Check your answer
Tree structure:
| Banquo | mistrusted | Macbeth | |
| [1] | [2] | ||
| PHON | < [4] Banquo > | < [5] mistrusted > | < [6] Macbeth > |
| HEAD | noun | [3] verb | noun |
| SUBJ | < > | < [1] NP[DR [a]] > | < > |
| SPR | < > | < > | < > |
| COMPS | < > | < [2] NP[DR [b]] > | < > |
| DR | [a]banquo | [c]mistrust2 | [b]macbeth |
| EX-C | ?? | [d] | ?? |
| PARTS | <banquo > | <mistrust2, mistrust2([a],[b]) > | <macbeth > |
| VP: mistrusted M. | S: B. mistrusted M. | |
| PHON | < [5], [6] > | < [4], [5], [6] > |
| HEAD | [3] | [3] |
| SUBJ | < [1] NP> | < > |
| SPR | < > | < > |
| COMPS | < > | < > |
| DR | [c] | [c] |
| EX-C | [d] | [d] |
| PARTS | <mistrust2, mistrust2([a],[b]) , | <mistrust2, mistrust2([a],[b]), |
| macbeth > | macbeth, banquo > |
Task 9: General mechanisms of LRS
1. Enumerate all possible logical forms that would be compatible with the PARTS lists of the sentence form Task 8.
2. Use the PARTS value from Task 8 to show that the following expressions are excluded as possible logical forms of the sentence.
(a) mistrust2(macbeth,banquo,banquo)
(b) mistrust2(banquo,banquo)
(c) macbeth(mistrust2,banquo)
Check your answer
(a) The expression cannot be a possible logical form, because it is not a well-formed formula: the predicate mistrust can only combine with two arguments, not with three. (This is indicated with the element mistrust2(...,...).
(b) The formula does not use all expressions from the PARTS list: the expression macbeth is missing.
(c) macbeth denotes an individual , mistrust2 is a predicate. Therefore, macbeth cannot function as predicate, not can mistrust2 function as its argument.
Task 10: Linking
Provide the full lexical entry of the verb from the sentence in Task 7 in such a way that it includes the linking information.
Check your answer
PHON < mistrusted >
HEAD verb