Wiki-ch2: Difference between revisions
| Line 55: | Line 55: | ||
[[File:Truthtable_NOT.png|300px]] | [[File:Truthtable_NOT.png|300px]] | ||
=== Truth tables for complex formulae === | |||
Truth tables are also useful to compute the truth value of complex formulae. | |||
This is shown in the following podcast, created by [[User:Lisa Lisa Günthner]]. | |||
<mediaplayer>http://www.youtube.com/watch?v=ZWdltj5Mqdc</mediaplayer> | |||
Revision as of 15:00, 11 April 2013
Additional Wiki pages for Chapter 2
Truth tables
Template:CreatedByStudentsWS1213
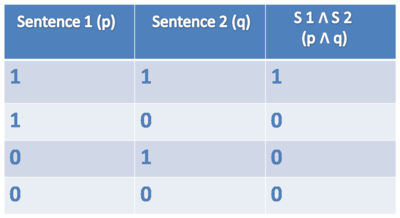
Truth tables for connectives
AND (∧)
Symbol: ∧
Sentence: Harry is a student and Snape is a teacher.
Formulae: student(harry) ∧ teacher(snape)
Truthtable AND
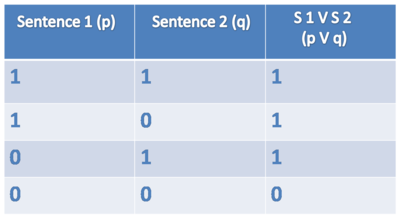
OR (∨)
Symbol: ∨
Sentence: Harry is a student or Snape is a teacher.
Formulae: student(harry) ∨ teacher(snape)
Truthtable OR
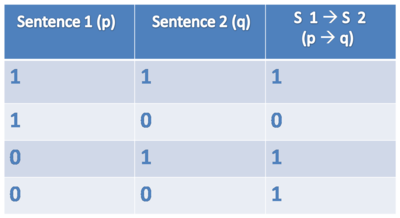
IF/THEN (⊃, →)
Symbol: ⊃, → (Note: We use the symbol ⊃ in the textbook as it is more common in the logical literature.)
Sentence: If Harry is a student then Snape is a teacher.
Formula: student(harry) ⊃ teacher(snape)
Truthtable IF/THEN
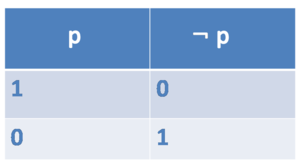
NOT (¬)
Symbol: ¬
Sentence: Harry is not a student.
Formula: ¬student(harry)
The original formula has to be false for the overall statement to be true.
Example: Only if student(harry) is false, ¬student(harry) is true.
Truthtable NOT
Truth tables for complex formulae
Truth tables are also useful to compute the truth value of complex formulae. This is shown in the following podcast, created by User:Lisa Lisa Günthner.
<mediaplayer>http://www.youtube.com/watch?v=ZWdltj5Mqdc</mediaplayer>