NMTS-Group9: Difference between revisions
| (107 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{MaterialUnderConstruction}} | {{MaterialUnderConstruction}} | ||
= Wikipage of Group | = Wikipage of Group 9 = | ||
== Overview == | == Overview == | ||
=== Members === | === Members === | ||
[[User:Lisa| Lisa]] <br /> [[User:Marthe| Marthe]] <br /> | '''[[User:Lisa| Lisa]]''' <br /> '''[[User:Marthe| Marthe]]''' <br /> '''[[User:Elisabeth.krall| Elisabeth]]''' <br /> '''[[User:IsaB|Isabelle]]''' | ||
=== Short description of the topic === | === Short description of the topic === | ||
'''Predicate logic - logical connectives''' | '''Predicate logic - logical connectives''' | ||
==== Examples ==== | "Predicate logic" is a linguistic concept belonging to the field of semantics, specifically syntax and grammar. Within that concept natural language is translated into a logical language (formulae) in order to illustrate the relation between a sentence, the conditions under which a given sentence is true and the circumstances in the real world. | ||
===== | |||
Symbol: Ʌ <br /> | |||
The predicate of a sentence serves either to assign an information (property) to a single argument ("argument" here meaning a part of the sentence, such as subjects and objects) or to relate two or more arguments to each other. The predicate is seen as linking its arguments to give purpose to a sentence's content. Such a sentence can be paraphrased in a structured way which gives information about the relations between the elements of the sentence. | |||
The purpose of Predicate logic is to avoid ambiguity in sentences by forming formulae out of natural language, which can only be interpreted in one way. Logical connectives, in form of symbols, are used to create formulae out of sentences with "and", "or", "if/then" and "not" and thereby giving information about the mentioned relations. | |||
The aim is to be able to interpret given formulae in a way that it becomes possible to state if a given sentence is true or false regarding a given model or story that the formulae were formed from. A model in this case means the information given about all the individuals of a setting, their properties and their relations in the real world. | |||
==== Connectives - Examples ==== | |||
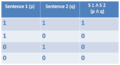
===== AND ===== | |||
Symbol: Ʌ <br /> | |||
Sentence: Harry is a student and Snape is a teacher. <br /> | Sentence: Harry is a student and Snape is a teacher. <br /> | ||
Formulae: [[student (harry) Ʌ teacher (snape)]] = true/false | Formulae: <nowiki>[[</nowiki>'''student(harry) Ʌ teacher(snape)''']] = ''true/false'' | ||
'''Truthtable AND''' | |||
[[File:Truthtable_AND1.png|400px]] | |||
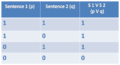
===== OR ===== | |||
Symbol: V <br /> | Symbol: V <br /> | ||
Sentence: Harry is a student or Snape is a teacher. <br /> | Sentence: Harry is a student or Snape is a teacher. <br /> | ||
Formulae: [[student (harry) V teacher (snape)]] = true/false | Formulae: <nowiki>[[</nowiki>'''student(harry) V teacher(snape)''']] = ''true/false'' | ||
'''Truthtable OR''' | |||
[[File:Truthtable_OR1.png|400px]] | |||
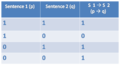
===== IF/THEN ===== | |||
Symbol: --> <br /> | Symbol: --> <br /> | ||
Sentence: If Harry is a student then Snape is a teacher. <br /> | Sentence: If Harry is a student then Snape is a teacher. <br /> | ||
Formulae: [[student (harry) --> teacher (snape)]] = true/false | Formulae: <nowiki>[[</nowiki>'''student(harry) --> teacher(snape''')]] = ''true/false'' | ||
'''Truthtable IF/THEN''' | |||
[[File:Truthtable_IF_THEN2.png|400px]] | |||
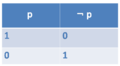
===== NOT ===== | |||
Symbol: ¬ <br /> | |||
Symbol: ¬ <br /> | |||
Sentence: Harry is not a student. <br /> | Sentence: Harry is not a student. <br /> | ||
Formulae: [[¬student (harry)]] = true/false | Formulae: <nowiki>[[</nowiki>'''¬student(harry)''']] = ''true/false'' | ||
The original formulae has to be false, that the overall statement is true. | |||
'''Example:''' | |||
Only if '''student(harry)''' is ''false'', '''¬student(harry''') is ''true''. | |||
'''Truthtable NOT''' | |||
[[File:Truthtable_NOT.png|300px]] | |||
==== Difficulties ==== | ==== Difficulties ==== | ||
| Line 39: | Line 84: | ||
* Understanding the whole process from creating a model to interpret formulae | * Understanding the whole process from creating a model to interpret formulae | ||
* Understanding the truth conditions of a formulae with connectives | * Understanding the truth conditions of a formulae with connectives | ||
== References and links == | == References and links == | ||
| Line 45: | Line 91: | ||
<!-- Indicate at least 3 references that you will use for your topic --> | <!-- Indicate at least 3 references that you will use for your topic --> | ||
* Course material "Introduction to Semantics" by Manfred Sailer | * Course material "Introduction to Semantics" by Manfred Sailer | ||
* Levine, Robert D., Frank Richter, and Manfred Sailer (in preparation): Formal Semantics. An Empirically Grounded Approach. Stanford: CSLI Publications. Draft of April 2012. | |||
=== Links === | === Links === | ||
[http://philosophy.hku.hk/think/sl/ | * [http://www.philosophy.hku.hk/think/sl Sentential Logic] | ||
* [http://www.philosophy.hku.hk/think/pl Predicate Logic] | |||
= Our e-learning objects = | = Our e-learning objects = | ||
| Line 59: | Line 106: | ||
<!-- List all the wiki pages that were created by your group. --> | <!-- List all the wiki pages that were created by your group. --> | ||
* in the Glossary: | * in the Glossary (only those relevant for our topic): | ||
** [[Glossary: | ** [[Glossary:_Predicate| Glossary entry for ''predicate'']] | ||
** [[Glossary: | ** [[Glossary:_Formulae| Glossary entry for ''formulae'']] | ||
** [[Glossary:_I-Function| Glossary entry for ''I-Function'']] | |||
** [[Glossary:_G-Function| Glossary entry for ''G-Function'']] | |||
** [[Glossary:_Logical Connectives| Glossary entry for ''Logical Connective'']] | |||
== Our | == Our podcast == | ||
<!-- List all the podcasts that were created by your group. --> | <!-- List all the podcasts that were created by your group. --> | ||
== Our | <embedvideo service="youtube" dimensions="400">http://youtu.be/4a3mXelw7H4</embedvideo> | ||
== Our material for an interactive whiteboard == | |||
<!-- List all the files that your group created for the interactive whiteboard. --> | <!-- List all the files that your group created for the interactive whiteboard. --> | ||
*[http://user.uni-frankfurt.de/~sailer/nmts-wise1213/Presentation-PredicateLogic.notebook Presentation on Predicate Logic] | |||
*[http://user.uni-frankfurt.de/~sailer/nmts-wise1213/Presentation-PredicateLogic-Comments.docx Comments on the presentation] | |||
== Our pictures == | == Our pictures == | ||
| Line 75: | Line 131: | ||
File:Lisa.jpg|Lisa | File:Lisa.jpg|Lisa | ||
File:MartheBerkenheide.jpg|Marthe | File:MartheBerkenheide.jpg|Marthe | ||
File: | File:IsabelleBrend'amour.jpg|Isabelle | ||
File:Truthtable_AND1.png|Truthtable AND | |||
File:Truthtable_OR1.png|Truthtable OR | |||
File:Truthtable_IF_THEN2.png|Truthtable IF THEN | |||
File:Truthtable_NOT.png|Truthtable NOT | |||
</gallery></nowiki> | </gallery></nowiki> | ||
--> | --> | ||
<gallery> | <gallery> | ||
File: | File:Truthtable_AND1.png|Truthtable AND | ||
File: | File:Truthtable_OR1.png|Truthtable OR | ||
File: | File:Truthtable_IF_THEN2.png|Truthtable IF THEN | ||
File:Truthtable_NOT.png|Truthtable NOT | |||
</gallery> | </gallery> | ||
== Our exercises == | == Our exercises == | ||
<!-- Provide links to all the exercises that your group has created.--> | <!-- Provide links to all the exercises that your group has created.--> | ||
Complex exercise on Predicate Logic: | |||
* [[Creation_of_the_World|Exercise 1: Creation of the World]] | |||
* [[Formulae_and_their_interpretation|Exercise 2: Formulae and their interpretation]] | |||
* [[Interpretation_of_formulae_with_connectives|Exercise 3: Interpretation of formulae with connectives]] | |||
Latest revision as of 22:23, 30 May 2018
Warning:
The material on this page has been created as part of a seminar. It is still heavily under construction and we do not guarantee its correctness. If you have comments on this page or suggestions for improvement, please contact Manfred Sailer.
This note will be removed once the page has been carefully checked and integrated into the main part of this wiki.
Wikipage of Group 9
Overview
Members
Lisa
Marthe
Elisabeth
Isabelle
Short description of the topic
Predicate logic - logical connectives
"Predicate logic" is a linguistic concept belonging to the field of semantics, specifically syntax and grammar. Within that concept natural language is translated into a logical language (formulae) in order to illustrate the relation between a sentence, the conditions under which a given sentence is true and the circumstances in the real world.
The predicate of a sentence serves either to assign an information (property) to a single argument ("argument" here meaning a part of the sentence, such as subjects and objects) or to relate two or more arguments to each other. The predicate is seen as linking its arguments to give purpose to a sentence's content. Such a sentence can be paraphrased in a structured way which gives information about the relations between the elements of the sentence.
The purpose of Predicate logic is to avoid ambiguity in sentences by forming formulae out of natural language, which can only be interpreted in one way. Logical connectives, in form of symbols, are used to create formulae out of sentences with "and", "or", "if/then" and "not" and thereby giving information about the mentioned relations.
The aim is to be able to interpret given formulae in a way that it becomes possible to state if a given sentence is true or false regarding a given model or story that the formulae were formed from. A model in this case means the information given about all the individuals of a setting, their properties and their relations in the real world.
Connectives - Examples
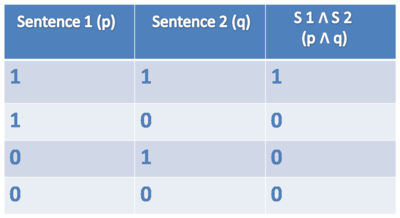
AND
Symbol: Ʌ
Sentence: Harry is a student and Snape is a teacher.
Formulae: [[student(harry) Ʌ teacher(snape)]] = true/false
Truthtable AND
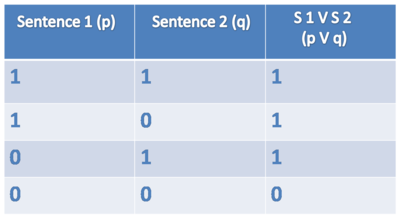
OR
Symbol: V
Sentence: Harry is a student or Snape is a teacher.
Formulae: [[student(harry) V teacher(snape)]] = true/false
Truthtable OR
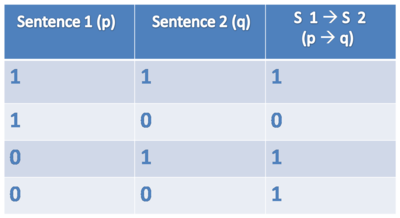
IF/THEN
Symbol: -->
Sentence: If Harry is a student then Snape is a teacher.
Formulae: [[student(harry) --> teacher(snape)]] = true/false
Truthtable IF/THEN
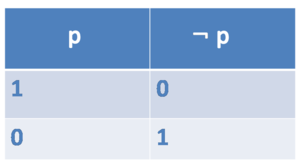
NOT
Symbol: ¬
Sentence: Harry is not a student.
Formulae: [[¬student(harry)]] = true/false
The original formulae has to be false, that the overall statement is true.
Example: Only if student(harry) is false, ¬student(harry) is true.
Truthtable NOT
Difficulties
- Abstraction of content/natural language
- Understanding the whole process from creating a model to interpret formulae
- Understanding the truth conditions of a formulae with connectives
References and links
References
- Course material "Introduction to Semantics" by Manfred Sailer
- Levine, Robert D., Frank Richter, and Manfred Sailer (in preparation): Formal Semantics. An Empirically Grounded Approach. Stanford: CSLI Publications. Draft of April 2012.
Links
Our e-learning objects
Our wiki pages
- in the Glossary (only those relevant for our topic):
Our podcast
Our material for an interactive whiteboard
Our pictures
Our exercises
Complex exercise on Predicate Logic: