NMTS-Group8

Warning:
The material on this page has been created as part of a seminar. It is still heavily under construction and we do not guarantee its correctness. If you have comments on this page or suggestions for improvement, please contact Manfred Sailer.
This note will be removed once the page has been carefully checked and integrated into the main part of this wiki.

(Back to the group overview)

Wikipage of Group 8

Overview

Members

• Ingo Müller
• Moonhwa Lindemann
• Boris Lehn
• Florian Bast
• Hilâl Ünal

Short description of the topic

Sorts:

In semantics, there are different sorts of entities. You distinguish between entities which represent a single person or object and entities that represent a group of persons/objects. Additionally, you differentiate between concrete and abstract entities. A concrete entity refers to a specific object, e.g. a particular being (which usually has a name); on the other hand, an abstract entity refers to a non-specific object.

Example:

The sentence The dodo is extinct refers to the entire species (of the dodo) and "the dodo" is therefore an abstract entity, i.e. a kind.
On the contrary, the sentence My dodo is extinct (or rather, dead), obviously neglecting the fact that dodos in general do not exist anymore, refers to a specific dodo, which thus is a concrete entity, i.e. an object.

The same goes for events. An event can be either concrete or abstract.

Types:

In logic and semantics a concept of type is often used to distinguish different kinds of expression (and of semantic value). These types are used as syntactic categories for the expressions in the semantic representation language. Each type will correspond to a certain set of possible denotations.
The (minimal) set of basic types is {e, t}:
– e (for entity) is the type of individual terms
– t (for truth value) is the type of formulae
All pairs <ϭ, τ> made up of (basic or complex) types ϭ, τ are types. <ϭ, τ> is the type of functions which map arguments of type ϭ to values of type τ.
In short: The set of types is the smallest set T such that e,tєT, and if ϭ,τ єT, then also <ϭ,τ> єT.

References and links

References

Kearns, K. (2000): Semantics
Lohnstein, H. (2011): Formale Semantik und natürliche Sprache

Links

The English Noun Phrase: an empirical study
UPPSALA UNIVERSITET - Algoritmer för datorlingvistisk semantik I
Zhaohui Luo - Word Meanings in Type-Theoretical Semantics

Our e-learning objects

Our wiki pages

• in the Glossary:
  • Glossary:Heteronym: the entry for Heteronymy
  • Glossary:Homonym: the entry for Homonymy
  • Glossary:Sorts/Types: the entry for Sorts/Types

Our podcasts

Sorts:

<mediaplayer>http://www.youtube.com/watch?v=EK6tqXdmFwk&feature=youtu.be</mediaplayer>

Our materials for an interactive whiteboard

Minipresentation on sorts

Presentation on types and sorts

Our pictures

• 

  IngoM

• Boris Profilbild.jpg

  BorisL

• 

  FlorianB

• 

  Hilâl

• 

  Moonhwa

Our exercises

Exercise I (Types)

Take a look at the following sentences! Which types does the word in italics require in each sentence?

1) Homer slept.
2) Homer choked Bart.
3) Moe sold beer to Homer.
4) Maggie hates Baby Gerald.

For the solutions, mark the following paragraph (which is seemingly empty) with your mouse.

1) <e,t> - sleep is an intransitive verb that does not require an object
2) <e,<e,t>> - choke is a transitive verb and requires a direct object
3) <e,<e,<e,t>>> - sell is a bi-transitive verb and requires a direct object as well as an indirect object
4) <e,<e,t>> - hate is a transitive verb and requires a direct object

Exercise II (Sorts)

Decide whether the words marked in italics in the following sentences refer to concrete/abstract single/group obejcts/events!

Example: The election of Mayor Quimby took place on Sunday.

Solution: The election of Mayor Quimby refers to a concrete (single) event.

1) Mr. Burns likes his nuclear power plant.
2) The Springfield Elementary students met at the gymnasium.
3) Nuclear meltdowns happen a lot in Springfield.
4) The three-eyed fish could be extinct soon.

For the solutions, mark the following paragraph (which is seemingly empty) with your mouse.

1) Mr. Burns refers to a concrete single object, i.e. an individual.
2) The Springfield Elementary students refers to a concrete group object, i.e. a group of individuals.
3) Nuclear meltdowns refers to an abstract group event.
4) The three-eyed fish refers to an abstract group object, i.e. a kind.

Exercise III (Types)

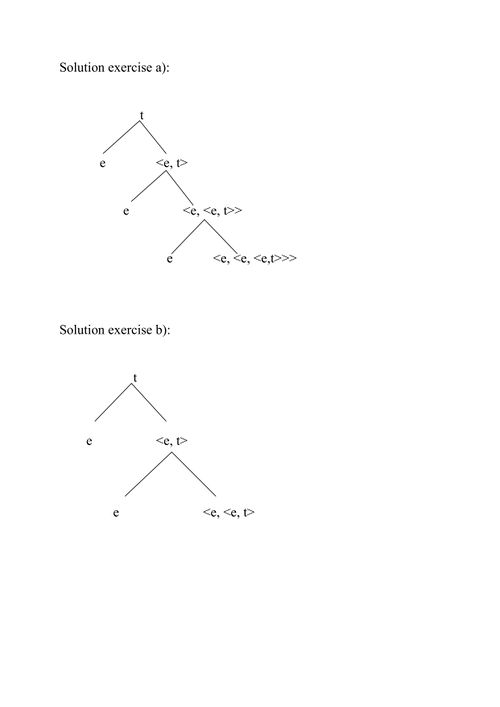
a) Draw a hierarchical tree of the predicate give’, which is of the type <e,<e,<e,t>>>:
b) Draw a hierarchical tree of the predicate kiss’, which is of the type <e,<e,t>>:
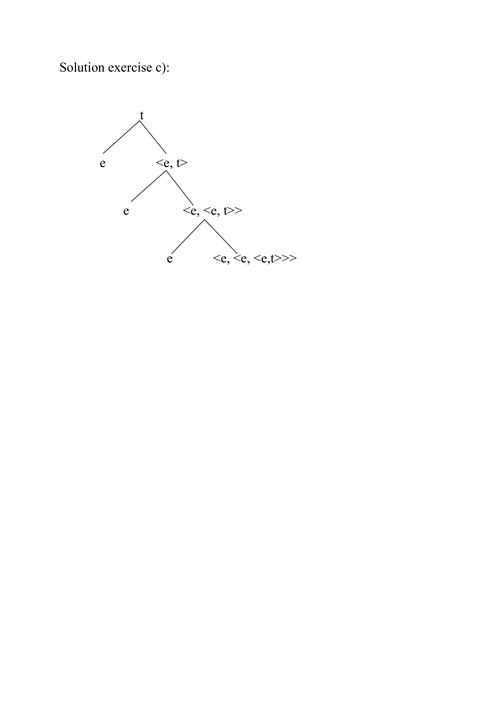
c) Draw a hierarchical tree of the predicate offer’, which is of the type <e,<e,<e,t>>>:

The solutions are displayed below.