Wiki-ch2

Additional Wiki pages for Chapter 2

Models

The following material is an adapted form of material created by student participants of the project e-Learning Resources for Semantics (e-LRS). Involved participants: Lisa, Marthe, Elisabeth, Isabelle.

Watch a short podcast what first-order models look like.

<mediaplayer>http://youtu.be/4a3mXelw7H4</mediaplayer>

Truth tables

The following material is an adapted form of material created by student participants of the project e-Learning Resources for Semantics (e-LRS). Involved participants: Lisa, Marthe, Elisabeth, Isabelle.

Truth tables for connectives

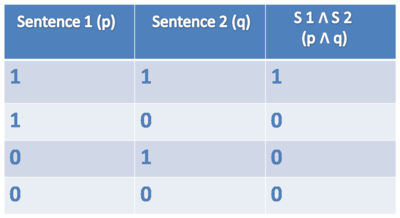
AND (∧)

Symbol: ∧
Sentence: Harry is a student and Snape is a teacher.
Formulae: student(harry) ∧ teacher(snape)

A conjunction p ∧ q it true if and only if p is true and q is true.

Truthtable AND

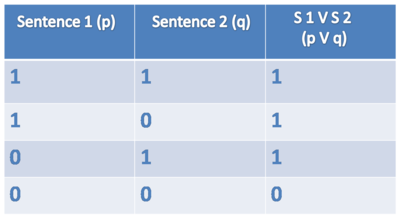
OR (∨)

Symbol: ∨
Sentence: Harry is a student or Snape is a teacher.
Formulae: student(harry) ∨ teacher(snape)

A disjunction p ∨ q is true if and only if p is true or q is true (or both).

Truthtable OR

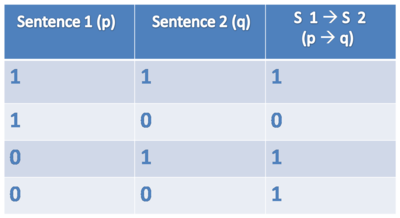
IF/THEN (⊃, →)

Symbol: ⊃, → (Note: We use the symbol ⊃ in the textbook as it is more common in the logical literature.)
Sentence: If Harry is a student then Snape is a teacher.
Formula: student(harry) ⊃ teacher(snape)

An implication p ⊃ q is true if and only if p is false or q is true (or both).
In other words: An implication p ⊃ q is true if and only if whenever p is true, q is true as well.

Truthtable IF/THEN

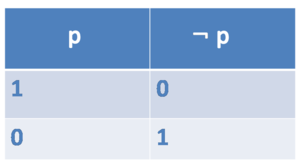
NOT (¬)

Symbol: ¬
Sentence: Harry is not a student.
Formula: ¬student(harry)

A negated formula ¬p is true if and only if p is false.

Example: Only if student(harry) is false, ¬student(harry) is true.

Truthtable NOT

Truth tables for complex formulae

Truth tables are also useful to compute the truth value of complex formulae. This is shown in the following podcast, created by Lisa Günthner.

<mediaplayer>http://www.youtube.com/watch?v=ZWdltj5Mqdc</mediaplayer>