Lara's Term Paper

Introduction to Quantifiers

The following e-learning material provides an introduction to the topic of quantifiers by integrating examples, illustrations as well as different types of interactive exercises of varying difficulty and their solutions. It intends to cover the central ideas of the concept of quantifiers without too much formal logic and therefore provides a basis for further study.

(Back to the Group Overview or Hauptseminar: "New Media in Teaching Semantics")

Wiki pages

Definition

A ‘quantifier’ is a word like many, few, little, several, which is used in a noun phrase to indicate the quantity of something.

In logic, quantifiers are operators binding variables, which means that a quantifier connects parts of a sentence that classify a domain of discourse.

Individual variables are written as “x” and can refer to any individual.

Different Types of Quantifiers

There are different types of quantifiers which can be divided in:

• Logical quantifiers
  • Universal quantifier
  • Existential quantifier
• Restricted quantifiers

In predicate logic the two fundamental quantifiers are the logical quantifiers (also called generalized quantifiers), which are the universal quantifier and the existential quantifier.

Logical Quantifiers (Generalized Quantifiers)

The Universal Quantifier ∀

• The universal quantifier is used to mean that the statement is true for every entity in the domain in question.
• symbolized by the operator ∀
• conveyed by such expressions as all, every and each
• The sequence “∀x” is read as
  • “For every thing x”
  • “For any value of x”
  • “For all values of x”
  • “Whatever x may be”

EXAMPLES

The following examples show quantified sentences translated into predicate logic formulae.

Every dog is barking.

∀x (DOG (x) → BARK (x))

“For every thing x, if x is a dog then x is barking.”

All students were tired.

∀x (STUDENT (x) → TIRED (x))

“For every thing x, if x is a student then x is tired.”

All bags which Jane carries are heavy.

∀x (BAG (x) & CARRY (Jane, x)) → HEAVY (x))

“For every thing x, if x is a bag and x is carried by Jane then x is heavy.”

The book was signed by every guest.

∀x (GUEST (x) → SIGN (x, the book))

“For all x, if x is a guest then x signed the book.”

Negation:

No trains are late.

Wherever you put an x, this statement does not hold:

∀x ~ (TRAIN (x) → LATE (x))

“It is not the case that for all x, if x is a train then x is late.”

Or equivalently, we can use the existential quantifier (see below) and say:

There is no x for which this statement would hold:

~ ∃x (TRAIN (x) & LATE (x))

“There is no x such that x is a train and x is late.”

The Existential Quantifier ∃

• The existential quantifier is used to mean that the statement is true of at least one entity in the domain.
• symbolized by the operator ∃
• stands for expressions with a/an (one), some and there is
• The sequence “∃x” is read as
  • “There is an x”
  • “There is at least one thing x”

Negation:

• The special case of the determiner no(ne) is analyzed with ∃ and negation.
• The sequence “~∃x” (same as “¬∃x”) is read as
  • “There is no x”

EXAMPLES

The following examples show quantified sentences translated into predicate logic formulae.

A dog barked.

∃x (DOG (x) & BARK (x))

“There is at least one thing x such that x is a dog and x barked.”

Anna bought some trashy paperbacks.

∃x (PAPERBACK (x) & TRASHY (x) & BUY (Anna, x))

∃x (PAPERBACK (x) & TRASHY (x) & BUY (a, x))

Note: In the second formula the variable a stands for ‘Anna’. Both of the writings are correct.

“There is an x such that x is a paperback and x is trashy and x is bought by Anna.”

Negation:

No trains are late.

There is no x for which this statement would hold:

~ ∃x (TRAIN (x) & LATE (x))

“There is no x such that x is a train and x is late.”

Or equivalently, we can use the universal quantifier (see above) and say:

Wherever you put an x, this statement does not hold:

∀x ~ (TRAIN (x) → LATE (x))

“It is not the case that for all x, if x is a train then x is late.”

There is no antidote to cyanide.

~ ∃x (ANTIDOTE (x, c))

„It is not the case that there is an x such that x is an antidote to cyanide.“ or „There is no x such that x is an antidote to cyanide.“

Clive ate nothing.

~ ∃x (EAT (c, x))

„There is no x such that Clive ate x.“

Clive didn’t eat one thing.

∃x ~ (EAT (c, x))

„There is at least one thing x such that Clive didn’t eat x.“

The Restricted Quantifier

In contrast to the logical quantifiers …

• a restricted quantifier always has a reference quantity and therefore points out a proportion of a set and not the proportion of everything there is.
• Since common natural language quantifiers like most, few, many or several cannot be analyzed like the logical quantifiers in the standard form of the predicate calculus, they are expressed in the notation of restricted quantification.
• Sentences which contain restricted quantifiers are written with square brackets. This means that the noun phrase including the quantifier is always put into square brackets. Logical quantifiers can also be written in this kind of formula with square brackets.
• Examples: a few – some – several – many – most – all – every – a – a number – one/two/three – little – no – no one – someone

EXAMPLES

The following examples show quantified sentences translated into predicate logic formulae.

Several cars crashed.

[Several x: CAR (x)] CRASH (x)

Maria peeled and quartered three apples.

[Three x: APPLE (x)] PEEL (m, x) & QUARTER (m, x)

Morris showed Jane every fingerprint he dusted.

[Every x: FINGERPRINT (x) & DUST (m, x)] SHOW (m, x, j)

Most travellers entering or leaving Australia visit Sydney.

[Most x: TRAVELLER (x) & (ENTER (x, a) or LEAVE (x, a))] VISIT (x, s)

[Most x: TRAVELLER (x) & (ENTER (x, a) V LEAVE (x, a))] VISIT (x, s)

Note: In the second formula the logical operator V means ‘or’. Both writings are correct.

Negation:

No dogs barked.

[No x: DOG (x)] BARK (x)

Venn Diagrams

• Generalized quantifiers can be treated as denoting a relation between two sets and can be illustrated by Venn diagrams.
• Two sets behave differently with respect to the necessity of being restricted.

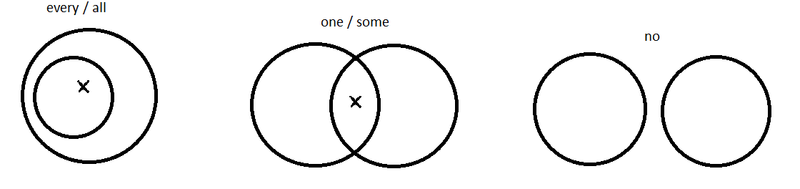
Representation of the basic quantifiers all (every), some (one), no(ne) in Venn diagrams:

In these diagrams, crosses are used to mark the presence of individuals in sets. Effectively the crosses play the role of variables – something which can stand in for any individual.

EXAMPLE

a. All Australians are sportspeople.

All denotes the subset relation between two sets – in the example given, the set of Australians and the set of sportsmen.

∀x (AUSTRALIANS (x) → SPORTSPERSON (x))

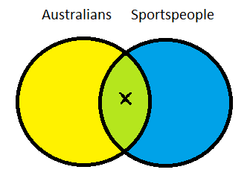
b. Some Australians are sportspeople.

Intersection:
The set of Australians and the set of sportspeople have an intersection.

∃x (AUSTRALIAN (x) & SPORTSPERSON (x))

c. No Australians are sportspeople.

No intersection

There is no x for which this statement would hold:

~ ∃x (AUSTRALIAN (x) & SPORTSPERSON (x))

“There is no x, such that x is an Australian and x is a sportsperson.”

Or equivalently, we can say:

Wherever you put an x, this statement does not hold:

∀x ~ (AUSTRALIANS (x) → SPORTSPERSON (x))

“It is not the case that for all x, if x is an Australian then x is a sportsperson.”

Representation of numerals in Venn diagrams:

Each numeral denotes a relation between sets such that the intersection contains the specific number of objects.

EXAMPLE

a. Five planets are visible to the naked eye.

Here it is indicated that there are five objects which are both planets and are visible to the naked eye. In other words the set of planets and the set of things which are visible to the naked eye have an intersection, and that intersection contains exactly five elements.

DRAWING

Scopal Ambiguity

Scopal ambiguity arises when a sentence contains two or more quantifiers. If this is the case the sentence can be understood in different ways.

Example: Some man loves every woman.

Two quantifiers: some and every

On the one hand you can read that there is a particular man who loves all women.

On the other hand you can read that every woman is loved by at least one man.

The different particular meanings can be clarified by expressing the scopal ambiguous sentence with the corresponding logical formulae. Each of these logical forms represents a particular meaning and thus cannot be ambiguous.

∃x (MAN (x) & ∀y (WOMAN (y) → LOVE (x, y)))

„There is a man such that he loves all women.“

∀x (WOMAN (x) → ∃y (MAN (y) & LOVE (y, x)))

„For every woman there is at least one man who loves her.“

References and Recommendations

References

• Cruse, Alan. 2006. A Glossary of Semantics and Pragmatics. Edinburgh: University Press.
• Gregory, Howard. 2000. Semantics. Language Workbook. London/New York: Rutledge.
• Gupta, C. B., S. R. Singh & Sandeep Kumar. 2011. Advance Discrete Structure. New Delhi: I.K. International Pvt. Ltd.
• Kearns, Kate. 2000. Semantics. Basingstoke: Macmillan.
• Lohnstein, Horst. 2011. Formale Semantik und natürliche Sprache (2nd ed.). Berlin/New York: De Gruyter.
• Portner, Paul H. 2005. What is Meaning? Fundamentals of Formal Semantics. Malden, MA [et al.]: Blackwell.
• Riemer, Nick. 2010. Introducing Semantics. Cambridge [et al.]: Cambridge University Press.
• Saeed, John Ibrahim. 2009. Semantics (3rd ed.). Malden, MA [et al.]: Wiley-Blackwell.
• Swan, Michael. 2005. Practical English Usage. 3rd edition. Oxford: Oxford University Press.
• von Heusinger, Klaus. 2001. “Book Review: Howard Gregory. 2000. Semantics (Language Workbooks). London: Routledge” in: Linguistics: An Interdisciplinary Journal of the Language Sciences, 39:4, 808-811. (accessed Apr/21/13 on http://www.ilg.uni-stuttgart.de/vonHeusinger/pub/index.php?sortieren=Publikationsart, pp. 1-4)

Online References

• Definition of Quantifier from the Oxford Online Dictionary
• Definition of Quantifier from the Stanford Encyclopedia of Philosophy
• Definition of Articles, Determiners and Quantifiers: http://grammar.ccc.commnet.edu/grammar/determiners/determiners.htm
• Explanation of Scopal Ambiguity: http://www.philosophyetc.net/2004/08/scopal-ambiguity.html

Recommendations for Reading

Gregory’s introductory book is not overwhelming through too much text but still thorough. It presents the central ideas and key concepts of semantic theory and is considerably tighter and more comprehensive by keeping things as informal as possible.

Gregory, Howard. 2000. Semantics. Language Workbook. London/New York: Rutledge.

• chap. 7 “Quantifiers (1)” (pp. 44-51) and chap. 8 “Quantifiers (2)” (pp. 52-56)

To build up on Gregory’s introduction and working at a higher level read through Kearn’s detailed and formally demanding chapters:

Kearns, Kate (2000): Semantics. Basingstoke: Macmillan.

• chap. 2.4 “The Logical Quantifiers” (pp. 41-51) and chap. 4 “Natural Language Quantifiers” (pp. 67-92)

Glossary Entries

Definitions in the Basic Glossary:

• Determiner
• Existential Quantifier
• Logical Form
• Logical Operator (Propositional Connective)
• Logical Quantifier
• Predicate Logic (First-order Logic)
• Quantifier
• Restricted Quantifier
• Scopal Ambiguity
• Universal Quantifier
• Variable

Online Excercises

Links to additionally created online exercises

Participants

• Lara

---

Back to the Group Overview or Hauptseminar: "New Media in Teaching Semantics"