Lara's Term Paper

Introduction to Quantifiers

The following e-learning material provides an introduction to the topic of quantifiers by integrating examples, illustrations as well as different types of interactive exercises of varying difficulty and their solutions. It intends to cover the central ideas of the concept of quantifiers without too much formal logic and therefore provides a basis for further study.

(Back to the Group Overview or Hauptseminar: "New Media in Teaching Semantics")

Wiki pages

Definition

A ‘quantifier’ is a word like many, few, little, several, which is used in a noun phrase to indicate the quantity of something.

In logic, quantifiers are operators binding variables, which means that a quantifier connects parts of a sentence that classify a domain of discourse.

Individual variables are symbols like “x”, "y" etc. and stand for the same entity each time they occur in a formula.

Different Types of Quantifiers

There are different types of quantifiers which can be divided in:

• Logical quantifiers
  • Universal quantifier
  • Existential quantifier
• Restricted quantifiers

In predicate logic the two fundamental quantifiers are the logical quantifiers, which are the universal quantifier and the existential quantifier.

Logical Quantifiers

The Universal Quantifier ∀

• The universal quantifier is used to mean that the statement is true for every entity in the domain in question.
• symbolized by the operator ∀
• conveyed by such expressions as all, every and each
• The sequence “∀x” is read as
  • “For every thing x”
  • “For any value of x”
  • “For all values of x”
  • “Whatever x may be”

EXAMPLES

The following examples show quantified sentences translated into predicate logic formulae.

Every dog is barking.

∀x (DOG (x) → BARK (x))

“For every thing x, if x is a dog then x is barking.”

All students were tired.

∀x (STUDENT (x) → TIRED (x))

“For every thing x, if x is a student then x is tired.”

All bags which Jane carries are heavy.

∀x (BAG (x) & CARRY (Jane, x)) → HEAVY (x))

“For every thing x, if x is a bag and x is carried by Jane then x is heavy.”

The book was signed by every guest.

∀x (GUEST (x) → SIGN (x, the book))

“For all x, if x is a guest then x signed the book.”

Negation:

No trains are late.

Wherever you put an x, this statement does not hold:

∀x ~ (TRAIN (x) → LATE (x))

“It is not the case that for all x, if x is a train then x is late.”

Or equivalently, we can use the existential quantifier (see below) and say:

There is no x for which this statement would hold:

~ ∃x (TRAIN (x) & LATE (x))

“There is no x such that x is a train and x is late.”

The Existential Quantifier ∃

• The existential quantifier is used to mean that the statement is true of at least one entity in the domain.
• symbolized by the operator ∃
• stands for expressions with a/an (one), some and there is
• The sequence “∃x” is read as
  • “There is an x”
  • “There is at least one thing x”

Negation:

• The special case of the determiner no(ne) is analyzed with ∃ and negation.
• The sequence “~∃x” (same as “¬∃x”) is read as
  • “There is no x”

EXAMPLES

The following examples show quantified sentences translated into predicate logic formulae.

A dog barked.

∃x (DOG (x) & BARK (x))

“There is at least one thing x such that x is a dog and x barked.”

Anna bought some trashy paperbacks.

∃x (PAPERBACK (x) & TRASHY (x) & BUY (Anna, x))

∃x (PAPERBACK (x) & TRASHY (x) & BUY (a, x))

Note: In the second formula the variable a stands for ‘Anna’. Both of the writings are correct.

“There is an x such that x is a paperback and x is trashy and x is bought by Anna.”

Negation:

No trains are late.

There is no x for which this statement would hold:

~ ∃x (TRAIN (x) & LATE (x))

“There is no x such that x is a train and x is late.”

Or equivalently, we can use the universal quantifier (see above) and say:

Wherever you put an x, this statement does not hold:

∀x ~ (TRAIN (x) → LATE (x))

“It is not the case that for all x, if x is a train then x is late.”

There is no antidote to cyanide.

~ ∃x (ANTIDOTE (x, c))

„It is not the case that there is an x such that x is an antidote to cyanide.“ or „There is no x such that x is an antidote to cyanide.“

Clive ate nothing.

~ ∃x (EAT (c, x))

„There is no x such that Clive ate x.“

Clive didn’t eat one thing.

∃x ~ (EAT (c, x))

„There is at least one thing x such that Clive didn’t eat x.“

The Restricted Quantifier

In contrast to the logical quantifiers …

• a restricted quantifier always has a reference quantity. The cardinal quantifiers can all be defined using exists and for all and only the proportional quantifiers actually require us to go beyond classical predicate logic.
• Since common natural language quantifiers like most, few, many or several cannot be analyzed like the logical quantifiers in the standard form of the predicate calculus, they are expressed in the notation of restricted quantification.
• Sentences which contain restricted quantifiers are written with square brackets. This means that the noun phrase including the quantifier is always put into square brackets. Logical quantifiers can also be written in this kind of formula with square brackets.
• Examples: a few – some – several – many – most – all – every – a – a number – one/two/three – little – no – no one – someone

EXAMPLES

The following examples show quantified sentences translated into predicate logic formulae.

Several cars crashed.

[Several x: CAR (x)] CRASH (x)

Maria peeled and quartered three apples.

[Three x: APPLE (x)] PEEL (m, x) & QUARTER (m, x)

Morris showed Jane every fingerprint he dusted.

[Every x: FINGERPRINT (x) & DUST (m, x)] SHOW (m, x, j)

Most travellers entering or leaving Australia visit Sydney.

[Most x: TRAVELLER (x) & (ENTER (x, a) or LEAVE (x, a))] VISIT (x, s)

[Most x: TRAVELLER (x) & (ENTER (x, a) V LEAVE (x, a))] VISIT (x, s)

Note: In the second formula the logical operator V means ‘or’. Both writings are correct.

Negation:

No dogs barked.

[No x: DOG (x)] BARK (x)

Venn Diagrams

• Generalized quantifiers can be treated as denoting a relation between two sets and can be illustrated by Venn diagrams.
• Two sets behave differently with respect to the necessity of being restricted.

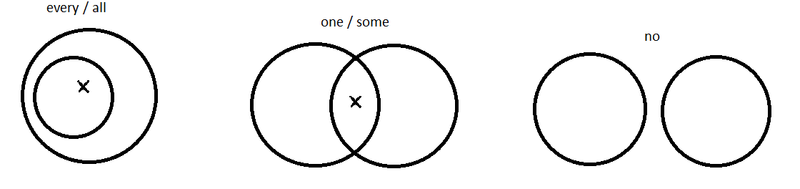
Representation of the basic quantifiers all (every), some (one), no(ne) in Venn diagrams:

In these diagrams, crosses are used to mark the presence of individuals in sets. Effectively the crosses play the role of variables – something which can stand in for any individual.

EXAMPLE

a. All Australians are sportspeople.

All denotes the subset relation between two sets – in the example given, the set of Australians and the set of sportsmen.

∀x (AUSTRALIANS (x) → SPORTSPERSON (x))

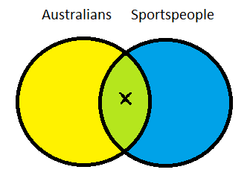
b. Some Australians are sportspeople.

Intersection:
The set of Australians and the set of sportspeople have an intersection.

∃x (AUSTRALIAN (x) & SPORTSPERSON (x))

c. No Australians are sportspeople.

No intersection

There is no x for which this statement would hold:

~ ∃x (AUSTRALIAN (x) & SPORTSPERSON (x))

“There is no x, such that x is an Australian and x is a sportsperson.”

Or equivalently, we can say:

Wherever you put an x, this statement does not hold:

∀x ~ (AUSTRALIANS (x) → SPORTSPERSON (x))

“It is not the case that for all x, if x is an Australian then x is a sportsperson.”

Representation of numerals in Venn diagrams:

Each numeral denotes a relation between sets such that the intersection contains the specific number of objects.

EXAMPLE

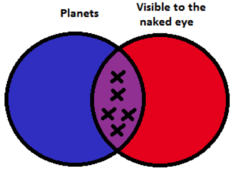
Five planets are visible to the naked eye.

Here it is indicated that there are five objects which are both planets and are visible to the naked eye. In other words the set of planets and the set of things which are visible to the naked eye have an intersection, and that intersection contains exactly five elements.

Scopal Ambiguity

Scopal ambiguity arises when a sentence contains two or more quantifiers. If this is the case the sentence can be understood in different ways.

Example: Some man loves every woman.

Two quantifiers: some and every

On the one hand you can read that there is a particular man who loves all women.

On the other hand you can read that every woman is loved by at least one man.

The different particular meanings can be clarified by expressing the scopal ambiguous sentence with the corresponding logical formulae. Each of these logical forms represents a particular meaning and thus cannot be ambiguous.

∃x (MAN (x) & ∀y (WOMAN (y) → LOVE (x, y)))

„There is a man such that he loves all women.“

∀x (WOMAN (x) → ∃y (MAN (y) & LOVE (y, x)))

„For every woman there is at least one man who loves her.“

References and Recommendations

References

• Cruse, Alan. 2006. A Glossary of Semantics and Pragmatics. Edinburgh: University Press.
• Gregory, Howard. 2000. Semantics. Language Workbook. London/New York: Rutledge.
• Gupta, C. B., S. R. Singh & Sandeep Kumar. 2011. Advance Discrete Structure. New Delhi: I.K. International Pvt. Ltd.
• Kearns, Kate. 2000. Semantics. Basingstoke: Macmillan.
• Lohnstein, Horst. 2011. Formale Semantik und natürliche Sprache (2nd ed.). Berlin/New York: De Gruyter.
• Portner, Paul H. 2005. What is Meaning? Fundamentals of Formal Semantics. Malden, MA [et al.]: Blackwell.
• Riemer, Nick. 2010. Introducing Semantics. Cambridge [et al.]: Cambridge University Press.
• Saeed, John Ibrahim. 2009. Semantics (3rd ed.). Malden, MA [et al.]: Wiley-Blackwell.
• Swan, Michael. 2005. Practical English Usage. 3rd edition. Oxford: Oxford University Press.
• von Heusinger, Klaus. 2001. “Book Review: Howard Gregory. 2000. Semantics (Language Workbooks). London: Routledge” in: Linguistics: An Interdisciplinary Journal of the Language Sciences, 39:4, 808-811. (accessed Apr/21/13 on http://www.ilg.uni-stuttgart.de/vonHeusinger/pub/index.php?sortieren=Publikationsart, pp. 1-4)

Online References

• Definition of Quantifier from the Oxford Online Dictionary
• Definition of Quantifier from the Stanford Encyclopedia of Philosophy
• Definition of Articles, Determiners and Quantifiers: http://grammar.ccc.commnet.edu/grammar/determiners/determiners.htm
• Explanation of Scopal Ambiguity: http://www.philosophyetc.net/2004/08/scopal-ambiguity.html

Recommendations for Reading

Gregory’s introductory book is not overwhelming through too much text but still thorough. It presents the central ideas and key concepts of semantic theory and is considerably tighter and more comprehensive by keeping things as informal as possible.

Gregory, Howard. 2000. Semantics. Language Workbook. London/New York: Rutledge.

• chap. 7 “Quantifiers (1)” (pp. 44-51) and chap. 8 “Quantifiers (2)” (pp. 52-56)

To build up on Gregory’s introduction and working at a higher level read through Kearn’s detailed and formally demanding chapters:

Kearns, Kate (2000): Semantics. Basingstoke: Macmillan.

• chap. 2.4 “The Logical Quantifiers” (pp. 41-51) and chap. 4 “Natural Language Quantifiers” (pp. 67-92)

Glossary Entries

Definitions in the Basic Glossary:

• Determiner
• Existential Quantifier
• Logical Form
• Logical Operator (Propositional Connective)
• Logical Quantifier
• Predicate Logic (First-order Logic)
• Quantifier
• Restricted Quantifier
• Scopal Ambiguity
• Universal Quantifier
• Variable

Online Excercises

Exercise 1: Venn Diagrams

Draw Venn diagrams illustrating the relations between sets which are claimed by the following sentences.

a. All students smoke (or: All students are smokers.)

Check your solution:

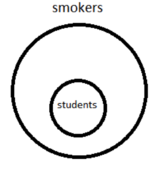
All denotes the subset relation between two sets – in the example given, the set of students and the set of smokers.
Suppose you can put a cross anywhere in the set of students. Wherever you put it, it is true that it will also be inside the set of smokers. This holds, in other words, ‘for all x’ (∀x). So the diagram is claiming that ‘for all x (assuming x is a student), x is a smoker’.

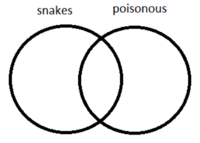
b. Some snakes are poisonous.

Check your solution:

The set of snakes and the set of things which are poisonous have an intersection.
In this diagram the assertion ‘x is a snake’ holds ‘for some x’ (∃x).

c. No cities are pleasant.

Check your solution:

In this diagram there is no intersection which means that there is no such x.
So it is not true that there is an x for which the assertion holds. Or wherever you put an x, it will not be the case that the assertion holds.

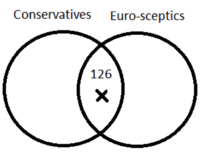
d. 126 Conservatives are Euro-sceptics.

Check your solution:

Here it is indicated that there are 126 objects which are both conservatives and Euro-sceptics. In other words the set of conservatives and the set of Euro-sceptics have an intersection, and that intersection contains exactly 126 elements.

Exercise 2: Logical Metalanguage "Warm-Up"

Translate following sentences into a logical metalanguage.

Example: Mulligan is asleep.

Possible answers:

• ASLEEP (Mulligan)
• ASLEEP (m)
• A (m)

1. Bill smokes.
2. Pete is crazier than Ryan.
3. Emma prefers Bill to Henry.
4. Mary doesn’t swim.
5. Fred smokes and Kate drinks.
6. If Ben drinks, Jenny gets angry.
7. Sarah was proud of the new car.
8. Sarah was proud that she graduated.

Check your solutions:

1. SMOKE (bill) or: SMOKE (b) or: S (b) (also in the following answers these writings are all correct)
2. CRAZIER (p, r)
3. PREFER (e, b, h)
4. ¬ SWIM (m)
5. SMOKE (f) & DRINK (k)
6. DRINK (b) → ANGRY (j)
7. PROUD (s, the new car)
8. PROUD (s, (GRATUATE (s))

Exercise 3: Different Types of Quantifiers (1)

Find the correct formula for the sentences below.

1 Utopia welcomes all travellers from Spain.

	∃x (TRAVELLER (x, from Spain) & WELCOME (Utopia, x))
	∀x (TRAVELLER (x, from Spain) → WELCOME (Utopia, x))
	[All x: TRAVELLER (x) & from Spain] WELCOME (Utopia, x))
	∀x (TRAVELLER (x, from Spain) & WELCOME (Utopia, x))

2 A black limousine awaited Marla.

	∃x (LIMOUSINE (x) & BLACK (x) & AWAIT (x, Marla))
	[An x: LIMOUSINE (x, black)] AWAIT (x, Marla)
	∀x (LIMOUSINE (x) & BLACK (x) → AWAIT (Marla))
	∃x (LIMOUSINE (x) & BLACK (x) → AWAIT (x))

3 Few paintings John owned were expensive.

	∃x (PAINTING (x) & OWN (j, x) → EXPENSIVE (x))
	∃x: PAINTING (x) & OWN (j, x) & EXPENSIVE (x)
	[Few x: PAINTING (x)] OWN (j, x) & EXPENSIVE (x)
	[Few x: PAINTING (x) & OWN (j, x)] EXPENSIVE (x)

Exercise 4: Different Types of Quantifiers (2)

Which type(s) of quantifiers do the sentences below have?

universal	existential	restricted
			1. Julie reads many books.
			2. All men are mortal.
			3. Some girl is nicer than Jane.
			4. There is a castle in Edinburgh.
			5. Three leaves fell.
			6. Clive gave a bone to every dog.
			7. Katie bathed the dog.
			8. Marcia liked most plays written by Osborne.

2. Write down the corresponding logical formula(e) for each sentence.

Check your solutions:

1. Julie reads many books.
   • Restricted quantifier: [Many x: BOOK (x)] READ (julie, x)
2. All men are mortal.
   • Universal quantifier: ∀x (MAN (x) → MORTAL (x))
   • Restricted quantifier: [All x: MAN (x)] MORTAL (x)
3. Some girl is nicer than Jane.
   • Existential quantifier: ∃x (GIRL (x) & NICER (x, jane))
   • Restricted quantifier: [Some x: GIRL (x)] NICER (x, jane)
4. There is a castle in Edinburgh.
   • Existential quantifier: ∃x (CASTLE (x, in Edinburgh))
   • Restricted quantifier: [An x: CASTLE (x, in Edinburgh)]
5. Three leaves fell.
   • Restricted quantifier: [Three x: LEAF (x)] FALL (x)
6. Clive gave a bone to every dog.
   • Universal quantifier: ∀x (DOG (x) → GIVE (clive, bone, x))
   • Restricted quantifier: [Every x: DOG (x)] GIVE (clive, bone, x)
7. Katie bathed the dog.
   • Existential quantifier: ∃x (DOG (x) & BATH (katie, x))
   • Restricted quantifier: [The x: DOG (x)] BATH (katie, x)
8. Marcia liked most plays written by Osborne.
   • Restricted quantifier: [Most x: PLAY (x) & WRITE (osborne, x)] LIKE (marcia, x)

Exercise 5: Logical Quantifiers

Using ∀ and ∃ where appropriate, write down the logical formulae for the following sentences and how each formula is read.

Example:
God made everything.
∀x (MAKE (g, x))
"For every thing x / For any value of x / Whatever x may be, God made x."

1. Somebody is speaking.
2. Harry loves everyone.
3. Everyone loves Harry.
4. Nobody is laughing.
5. All monkeys are clever.
6. There exists a unicorn.
7. Every student knows the professor.
8. The professor knows every student.
9. Ida saw something sinister.
10. All crowded cities are dangerous.
11. A young woman arrived.

Check your solutions:

1. Somebody is speaking.

   ∃x (SPEAK (x))

   "There is an x / There is at least one thing x, such that x is speaking."

2. Harry loves everyone.

   ∀x (LOVE (harry, x)

   "For every thing x, Harry loves x."

3. Everyone loves Harry.

   ∀x (LOVE (x, harry)

   "For all values of x, x loves Harry."

4. Nobody is laughing.

   ~∃x (LAUGH (x)) or: ∀x ~(LAUGH (x)

   "There is no x such that x is laughing. / It is not the case that for all x that x is laughing."

5. All monkeys are clever.

   ∀x (MONKEY (x) → CLEVER (x))

   "For every thing x, if x is a monkey then x is clever."

6. There exists a unicorn.

   ∃x (UNICORN (x))

   “There is at least one thing x such that x is a unicorn.”

7. Every student knows the professor.

   ∀x (STUDENT (x) → KNOW (x, professor)

   "For every thing x, if x is a student then x knows the professor."

8. The professor knows every student.

   ∀x (STUDENT (x) → KNOW (professor, x)

   "For every thing x, if x is a student then x knows the professor."

9. Ida saw something sinister.

   ∃x (SINISTER (x) & SEE (Ida, x))

   “There is an x such that x is sinister and x is seen by Ida.”

10. All crowded cities are dangerous.

    ∀x (CITY (x) & CROWDED (x)) → DANGEROUS (x))

    "For every thing x, if x is a city and x is crowded then x dangerous."

11. A young woman arrived.

    ∃x (WOMAN (x) & YOUNG (x) & ARRIVE (x))

    “There is an x such that x is a woman and x is young and x arrives.”

Extra:
Write the following as predicate-argument using ∀ and ∃ where appropriate.

1. Maxime sent every letter John had written her to Ruth.
2. Gina or Boris fed every puppy.
3. No trains are late.
4. No beautiful women like John.
5. Every student reads some book by Shakespeare.
6. Everyone who admires someone does not despite that person.

Check your solutions:

1. Maxime sent every letter John had written her to Ruth.

   ∀x (LETTER (x, written by John to Maxime) → SEND (Maxime, x, Ruth))

2. Gina or Boris fed every puppy.

   ∀x (PUPPY (x) → FEED (Gina, x) or FEED (Boris, x))

3. No trains are late.

   ~∃x (TRAIN (x) & LATE (x)) or ∀x ~ (TRAIN (x) → LATE (x))

4. No beautiful women like John.

   ~∃x ((WOMAN (x) & BEAUTIFUL (x)) & LIKE (x, john))

5. Every student reads some book by Shakespeare.

   ∀x (STUDENT (x) → ∃y (BOOK (y) & READ (x, y)))

6. Everyone who admires someone does not despite that person.

   ∀x ∀y (ADMIRE (x, y) → ~ DESPITE (x, y))

Exercise 6: Restricted Quantifiers

Using restricted quantifier notation, give the formulae for the sentences below.

Example:
John photographed every model that Bill hired.
[Every x: MODEL (x) & HIRE (b, x)] PHOTOGRAPH (j, x)

1. Anna has read most books on phsychoanalysis.
2. Few who knew him supported Baxter.
3. Some students who heard both concerts were interviewed by Holmes.
4. Kyle showed Lucie every fingerprint he dusted.
5. Mary peeled and quartered three apples.
6. Ryan ate a peanut.
7. Victor signs every sculpture he makes.
8. Mary and Charles ate four apples each.
9. Jane restored and sold several valuable paintings.
10. Most bulbs will not grow if they are dry.
11. Most travellers entering or leaving Australia visit Sydney.

Check your solutions:

1. Anna has read most books on psychoanalysis.

   [Most x: BOOK (x) & PSYCHOANALYSIS (x)] READ (a, x)

2. Few who knew him supported Baxter.

   [Few x: KNOW (x, b)] SUPPORT (x, b)

3. Some students who heard both concerts were interviewed by Holmes.

   [Some x: STUDENT (x) & HEAR (x, c)] INTERVIEW (h, x)

4. Kyle showed Lucie every fingerprint he dusted.

   [Every x: FINGERPRINT (x) & DUST (m, x)] SHOW (k, x, l)

5. Mary peeled and quartered three apples.

   [Three x: APPLE (x)] PEEL (m, x) & QUARTER (m, x)

6. Ryan ate a peanut.

   [An x: PEANUT (x)] EAT (r, x)

7. Victor signs every sculpture he makes.

   [Every x: SCULPTURE (x) & MAKE (r, x)] SIGN (v, x)

8. Mary and Charles ate four apples each.

   [Four x: APPLE (x)] EAT (m, x) & EAT (c, x)

9. Jane restored and sold several valuable paintings.

   [Several x: PAINTING (x) & VALUABLE (x)] RESTORE (j, x) & SELL (j, x)

10. Most bulbs will not grow if they are dry.

    [Most x: BULB (x) & DRY (x)] ~GROW (x)

11. Most travellers entering or leaving Australia visit Sydney.

    [Most x: TRAVELLER (x) & (ENTER (x, a) V LEAVE (x, a))] VISIT (x, s)
    

or: [Most x: TRAVELLER (x) & (ENTER (x, a) or LEAVE (x, a))] VISIT (x, s)

Exercise 7: First-Order Logic "Mix"

Translate the sentences below into first-order logic.

1. Kate was a liberal but Andrew was a socialist.
2. You can if you try.
3. Every baby cried.
4. Someone is conservative.
5. John likes many animals.
6. No honest politicians are businessmen.
7. If Thomas snores, then Maria hates Thomas.
8. Thomas doesn’t snore.
9. All dishes which Anna cooks are delicious.
10. Four politicians are honest.
11. No guy likes Lisa.
12. All students who know John know Mary.
13. Several students who drink tequila dance.
14. Not many books James owned were expensive.
15. Some tourists who visit London are rich.
16. Nobody loves everybody.
17. If everybody loves everybody, then everybody loves him/herself.
18. If all students flunk, no student will be glad.

Check your solutions:

1. Kate was a liberal but Andrew was a socialist.

   LIBERAL (k) & SOCIAL (a) or: LIBERAL (kate) & SOCIAL (andrew)) or: L (k) & S (a)) (also in the following answers these writings are all correct)

2. You can if you try.

   TRY (x) → CAN (x)

3. Every baby cried.

   ∀x (BABY (x) → CRY (x))

4. Someone is conservative.

   ∃x (CONSERVATIVE (x))

5. John likes many animals.

   [Many x: ANIMAL] LIKE (john, x)

6. No honest politicians are businessmen.

   ~∃x ((POLITICIAN (x) & HONEST (x)) & BUSINESSMAN (x))

7. If Thomas snores, then Maria hates Thomas

   SNORE (thomas) → HATE (maria, thomas)

8. Thomas doesn’t snore.

   ~ (SNORE (thomas))

9. All dishes which Anna cooks are delicious.

   ∀x (DISH (x) & COOK (anna, x)) → DELICIOUS (x))

10. Four politicians are honest.

    [Five x: POLITICIAN] HONEST (x)

11. No guy likes Lisa.

    ~ ∃x (GUY (x) & LIKE (x, lisa)) or: ∀x ~ (GUY (x) → LIKE (x, lisa))

12. All students who know John know Mary.

    ∀x (STUDENT (x) & KNOW (x, john)) → KNOW (x, mary))

13. Several students who drink tequila dance.

    [Several x: STUDENT (x) & DRINK (x, tequila)] DANCE (x)

14. Not many books James owned were expensive.

    [Not many x: BOOK (x) & OWN (james, x)] EXPENSIVE (x)

15. Some tourists who visit London are rich.

    ∃x (TOURIST (x) & VISIT (x, london) & RICH (x))

16. Nobody loves everybody.

    ~ (∃x (∀y (LOVE (x, y))))

17. If everybody loves everybody, then everybody loves him/herself.

    ∀x (∀y (LOVE (x, y) → LOVE (x, x)))

18. If all students flunk, no student will be glad.

    ∀x (STUDENT (x) → FLUNK (x) → ~ ∃x (STUDENT (x) & GLAD (x))

Exercise 8: Paraphrasing into Plain English

What do the following logical formulae mean in plain English?

Example:
∃x (CHILD (x) & SLEEP (x))
A child sleeps. / A child slept. (also in the following answers several writings are correct)

1. ∀x (STUDENT (x) → KNOW (x, mary))
2. ∃x (KILL (robert, x))
3. ~ ∃x (KNOW (x, bill))
4. ∀x ~ (FORGET (x, lisa))
5. ADMIRE (burt, frank) & DESPITE (frank, burt)
6. [Most x: DOG (x)] DOMESTIC (x)
7. ∀x ~ (NEWSPAPER (x) & READ (john, x))
8. ∀x ((SKODA (x) & RED (X)) → WORK (x))
9. [Four x: APPLE (x)] EAT (marcia, x) & EAT (clive, x)
10. ∀y (∃x (MAN (x) & (WOMAN (y) → LOVE (x, y))))

Check your solutions:

1. Every student knows Mary. (All students know Mary.)
2. Robert kills somebody.
3. Nobody knows Bill.
4. Nobody forgets Lisa.
5. Burt admires Frank but Frank despite Burt.
6. Most dogs are domestic.
7. John reads no newspaper. (John doesn’t read any newspaper.)
8. All red sodas work.
9. Marcia and Clive eat four apples each.
10. One man loves every woman.

Exercise 9: Scopal Ambiguity

1. In which way is the following sentence ambiguous?
2. Write down the two possible logical forms.

Everyone loves someone.

One Reading

Another Reading

Check your solution for 1:

In this sentence, the scopal ambiguity is created by the two quantifiers everyone and someone.
When looking at the two pictures that try to help you, you can see two possible readings:

1. For every person there is, there is at least one other person who loves him / her.
2. There is one person that is loved by everyone else.

Check your solution for 2:

1. For every person there is at least one person who loves him / her:

   ∀x (PERSON (x) → ∃y (PERSON (y) & LOVE (x, y))

2. There is one person that is loved by everyone:

   ∃x (PERSON (x) → ∀y (PERSON (y) & LOVE (y, x))

Participants

• Lara

---

Back to the Group Overview or Hauptseminar: "New Media in Teaching Semantics"