Semantics 1, WiSe 1718
General information
Course description
Semantics is the study of the (literal) meaning of words and sentences. The meaning of a sentence is usually predictable from the words in the sentence and its syntactic structure. Yet, this relationship between form and meaning is not a simple one-to-one mapping. Instead, it is rich in ambiguities, pleonastic marking and elements without any identifiable meaning contribution. We will work on an account that is founded on classical tools of semantic research but still directly addresses these empirical challenges. After the class, the participants will be able to identify - and partly analyze - interesting semantic phenomena in naturally occurring texts. They will have acquired a basic working knowledge in formal logic, which they will be able to apply in the description of meaning
Time and place
- Tuesday 08:15-9.45
- Starting: 17.10.2017
- Room: IG 3.201 (IG-Farben-Haus)
Modules
- Lehramt Englisch (L2/5, L3): FW2
- BA English Studies: 3.4(1)
- BA Empirische Sprachwissenschaft: K 6.1, En 4.1, DH 6.1
Contact
Manfred Sailer
e-mail: sailer@em.uni-frankfurt.de
office: IG 3.214
office hours: contact via e-mail!
www: http://user.uni-frankfurt.de/~sailer/index.htm
Course requirements
L2 and L5
- regular attendance
- pass all assignment sheets
- Modulprüfung (optional): 90 min written exem (2 CP)
L3
- regular attendance
- pass all assignment sheets
- Modulprüfung (optional):
- 20 min. oral exam
- not possible: kleine Hausabeit
BA English Studies
- regular attendance
- pass all assignment sheets
- literary scenario:
- Part 1: Extract 15 ambiguous sentences from the text such that all types of ambiguity covered in class are represented provide unambiguous paraphrases of the readings determine the type of ambiguity
- Part 2:
- Define a formal model consisting of 3 characters from your text, which contains 2 properties, 1 2-place relation
- Formulate 2 atomic formulae and compute their truth value.
- Formulate 4 complex formulae with at least 1 logical connective in each and compute their truth value.
- Formulate 1 complex formula with at least 2 logical connectives in
it and compute its truth value.
BA Empirische Sprachwissenschaft
K 6.1
- regular attendance
- Modulprüfung (obligatory): 90min. written exam
En 4.2
- regular attendance
- pass all assignment sheets
- literary scenario
DH 6.1
to be added
Erasmus 6 CP
- regular attendance
- pass the assignment sheets
- 90min. written exam
- small literary scenario:
- Part 1: Extract 4 ambiguous sentences from the text such that different types of ambiguity covered in class are represented provide unambiguous paraphrases of the readings determine the type of ambiguity
- Part 2:
- Define a formal model consisting of 3 characters from your text, which contains 2 properties, 1 2-place relation
- Formulate 2 atomic formulae and compute their truth value.
- Formulate 2 complex formulae with at least 1 logical connective in each and compute their truth value.
- Formulate 1 complex formula with at least 2 logical connectives in
it and compute its truth value.
The grade will be determined by the result of the written exam.
Assignment sheets
Assignment sheet 1: File:WiSe1718-assignment-logic.pdf
Assignment sheet 2: File:WiSe1718-assignment-lrs.pdf
Mock exam: File:WiSe1718-mockexam.pdf
Mock exam
The examples in the text are based on Shakespeare's play Macbeth. The full text of the play is available on Projekt Gutenberg.
We will use the TV show The Fresh Prince of Bel-Air for the final exam this term.
Task 1: Ambiguity
Consider the following ambiguous sentences. For each of them, provide an unambiguous paraphrase for the possible readings.
(1) a. Duncan trusted Macbeth because he was a thane.
Check your answer
Reading 1: he refers to Macbeth. Paraphrase: Duncan trusted Macbeth because Macbeth was a thane.
Reading 2: he refers to Duncan. Paraphrase: Duncan trusted Macbeth because Duncan was a thane.
b. Every king trusts a thane.
Check your answer
Reading 1: every takes scope over a. Paraphrase: For every king there is at least one thane such that the king trusts that thane.
Reading 2: a takes scope over every. Paraphrase: There is one particular thane such that each king trusts this thane.
b. Macbeth and Macduff are married.
Check your answer
Reading 1: collective reading. Paraphrase: Macbeth and Macduff are married to each other
Reading 2: distributive reading. Paraphrase: Macbeth and Macduff are both married, but not to each other.
b. Macbeth killed a king with a dagger.
Check your answer
Reading 1: the PP with a dagger is a modifier of the verb kill Paraphrase: Macbeth used a dagger to kill a king.
Reading 2: the PP with a dagger is a modifier of the noun king. Paraphrase: Macbeth killed a king who had a dagger.
Task 2: Model and Interpretation
1. Define a universe that consists of Macbeth and Banquo.
Check your answer
U = { Macbeth, Banquo }
2. Define the interpretation of the names macbeth and banquo in an intuitively plausible way.
Check your answer
I(macbeth) = Macbeth,
I(banquo) = Banquo
3. Define the interpretation of the properties thane1, king1, and witch1 is such a way that Macbeth is a king, both are thanes and neither is a witch.
Check your answer
I(thane1) = {<Macbeth>, <Banquo>},
I(king1) = {<Macbeth>},
I(witch1) = {}
4. Define the interpretation of the 2-place relations mistrust2 and kill2 in such a way that Macbeth and Banquo mistrust each other and Macbeth kills Banquo.
Check your answer
I(mistrust2) = {<Macbeth, Banquo>, <Banquo, Mactbeth>},
I(kill2) = {<Macbeth,Banquo>}
Task 3: Formulae
Write down logical formulae that express the meaning of the following sentences.
1. Banquo is a thane.
Check your answer
thane1(banquo)
2. Macbeth is king and Macbeth mistrusts Banquo.
Check your answer
king1(macbeth) ∧ mistrust2(macbeth,banquo)
3. If Banquo is king then Macbeth does not kill Banquo.
Check your answer
king1(banquo) ⊃ ¬ kill2(macbeth,banquo)
Task 4: Interpreting formulae
Compute the interpretation of the following formulæ step by step.
1. mistrust2(macbeth,macbeth)
Check your answer
[[mistrust2(macbeth,macbeth)]] = 1
iff < [[macbeth]], [[macbeth]] > is in [[mistrust2]]
iff < I(macbeth), I(macbeth) > in I(mistrust2)
iff < Macbeth, Macbeth > in { <x,y> | x mistrusts y } = { <Macbeth, Banquo>, <Banquo, Macbeth> }
Since this is not the case, [[mistrust2(macbeth,macbeth)]] = 0.
2. ¬king(banquo)
Check your answer
[[¬ king1(banquo)]] = 1
iff [[king(banquo)]] = 0
iff < [[banquo]]> is not in [[king1]]
iff < I(banquo> is not in I(king1)
iff < Banquo > is not in { <x> | x is king } = { <Macbeth>}
Since this is the case, [[¬ king1(banquo)]] = 1
3. witch1(banquo) ⊃ king1(macbeth)
Check your answer
[[witch1(banquo) ⊃ king1(macbeth))]] = 1
iff [[witch1(banquo)]] = 0 or [[king1(macbeth) = 1
iff < [[banquo]] > is not in [[witch1]] or < [[macbeth]] > is in [[king1]]
iff < I(banquo) > is not in I(witch1) or < I(macbeth) > is in I(king1)
iff < Banquo > is not in { <x> | x is a witch} = { } or < Macbeth > is in { <x> | x is king} = { <Macbeth>}.
Since both are the case, [[witch1(banquo) ⊃ king1(macbeth))]] = 1.
Task 5: Variables
Provide a g-function that maps the variables x, y, and z to individuals from the universe and compute the interpretation of the following formula with respect to the model and your g.
(i) kill2(z,x)
Check your answer
Example solution (other values for g are equally possible).
g(x) = Macbeth,
g(y) = Banquo,
g(z) = Banquo.
With this variable assignment we can compute the truth value of the formula:
[[kill2(z,x)]]g = 1
iff < [[z]]g, [[x]]g > is in [[kill2]]g
iff < g(z), g(x) > is in I(kill2)
iff < Banquo, Macbeth > is in { <x,y> | x killed y} = { <Macbeth, Banquo> }.
Since this is not the case, [[kill2(z,x)]]g = 0.
Task 6: Quantifiers
Provide logical formulae that expresse the meaning of the following sentences. Are the formulae true in your model (not in the entire play)? Give a short reason (you don’t need to compute the truth value).
1. Banquo was killed by a king.
Check your answer
∃x (king(x) : kill(x, banquo))
The formula is true in my model, because there is only one king, Macbeth, and Macbeth killed Banquo.
(Note: The English sentence is in passive, but this has no effect on the logical form.)
2. Macbeth mistrusts every witch.
Check your answer
∀x (witch(x) : mistrust(macbeth, x))
The formula is true in my model, because there are no witches in my model. Therefore, the formula with the universal quantifier is trivially true.
Task 7: Analysis
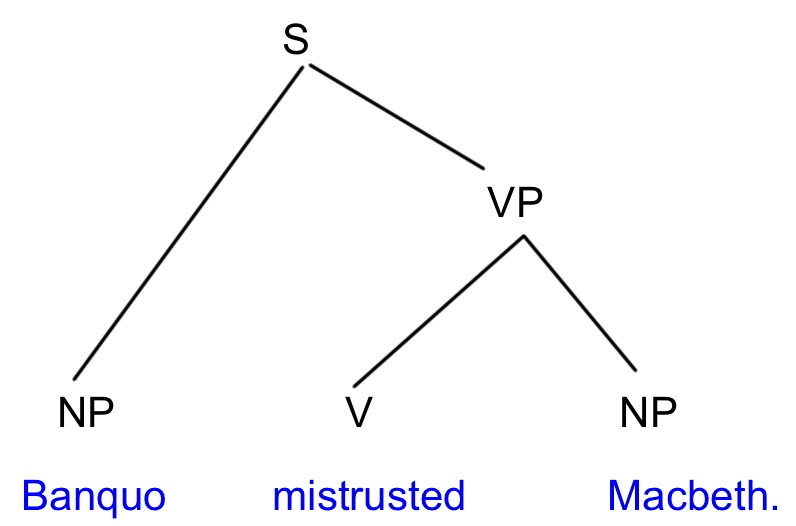
Provide the lexical entries for the words in the sentence Banquo mistrusted Macbeth. Use the features PHON, HEAD, SUBJ, SPR, COMPS, DR, PARTS, and EX-CONT.
Check your answer
| Banquo | mistrusted | Macbeth | |
| [1] | [2] | ||
| PHON | < Banquo > | < mistrusted > | < Macbeth > |
| HEAD | noun | verb | noun |
| SUBJ | < > | < NP[DR [a]] > | < > |
| SPR | < > | < > | < > |
| COMPS | < > | < NP[DR [b]] > | < > |
| DR | [a]banquo | [c]mistrust2 | [b]macbeth |
| EX-C | ?? | ?? | ?? |
| PARTS | < [a]banquo > | < [b]mistrust2, [b]([a],[c]) > | <[c]macbeth > |
Task 8: Analysis
Provide the full HPSG and LRS analysis of the sentence Banquo mistrusted Macbeth. Use the features PHON, HEAD, SUBJ, SPR, COMPS, DR, PARTS, and EX-CONT. You only need to mention the EX-CONT value at the highest node in the tree.
Check your answer
Tree structure:
| Banquo | mistrusted | Macbeth | |
| [1] | [2] | ||
| PHON | < [4] Banquo > | < [5] mistrusted > | < [6] Macbeth > |
| HEAD | noun | [3] verb | noun |
| SUBJ | < > | < [1] NP[DR [a]] > | < > |
| SPR | < > | < > | < > |
| COMPS | < > | < [2] NP[DR [b]] > | < > |
| DR | [a]banquo | [c]mistrust2 | [b]macbeth |
| EX-C | ?? | [d] | ?? |
| PARTS | <banquo > | <mistrust2, mistrust2([a],[c]) > | <macbeth > |
| VP: mistrusted M. | S: B. mistrusted M. | |
| PHON | < [5], [6] > | < [4], [5], [6] > |
| HEAD | [3] | [3] |
| SUBJ | < [1] NP> | < > |
| SPR | < > | < > |
| COMPS | < > | < > |
| DR | [c] | [c] |
| EX-C | [d] | [d] |
| PARTS | <mistrust2, mistrust2([a],[c]) , | <mistrust2, mistrust2([a],[c]), |
| macbeth > | macbeth, banquo > |
Task 8': Principles of syntax
1. How is the COMPS value of the VP determined by the lexical entries of the words and the principles of grammar?
Check your answer
The VP is licenced as a head-complement structure. The constraint on head-complement structures requires that the head daughter have a non-empty COMPS list and the mother have an empty COMPS list.
(It is also required that the non-head daughters are identical to the elements on the head daughter's COMPS list, but this is not relevant for the question at hand.)
2. How is it guaranteed that the PHON values of the words all appear in the PHON value of the sentence?
Check your answer
The Phonology Principle specifies that the PHON value of a mother is the concatenation of the PHON values of its daughter(s). Therefore, a element of the PHON value of a word in a sentence will always be part of the PHON values of every phrase that dominates this word. Since the overall sentence dominates all its component words, its PHON value comprises the PHON values of all words of this sentence.
3. How is it achieved that the HEAD value of the sentence is verb?
Check your answer
The HEAD value of the lexical verb, mistrust, is verb. In the VP, the lexical verb is the syntactic head of the phrase. According to the Head Feature Priniciple, the HEAD value of the mother node is the same as that of its head daughter, i.e., verb. Since this VP is the headdaughter of the sentence, the sentence's HEAD value should also be the same, i.e., verb again.
Task 9: General mechanisms of LRS
Explain how the following formulae are excluded from occurring as EX-CONT values of the sentence from Task 7.
(a) mistrust2(macbeth,banquo,banquo)
(b) mistrust2(banquo,banquo)
(c) macbeth(mistrust2,banquo)
(d) mistrust2(macbeth,banquo)
Check your answer
(a) The expression cannot be a possible logical form, because it is not a well-formed formula: the predicate mistrust can only combine with two arguments, not with three. (This is indicated with the element mistrust2(...,...).
(b) The formula does not use all expressions from the PARTS list: the expression macbeth is missing.
(c) macbeth denotes an individual , mistrust2 is a predicate. Therefore, macbeth cannot function as predicate, not can mistrust2 function as its argument.
(d) The subject, Banquo, should be linked to the first semantic argument slot of the predicate mistrust2 - analogously for the complement and the second argument slot of the predicate. This is specified in the lexical entry of the verb, where the DR values of the subject ([a]) and the complement ([b]) are identified with the first and the second argument slots of mistrust2 respectively.
Material for week 14 (30.1.2018)
Possible EX-CONT values
Given the following PARTS lists, what are possible EX-CONT values (if we do not assume other restrictions)
1. PARTS < pat, alex,like, like(__,__) >
Check your answer
like(pat,alex)
like(alex,pat)
2. PARTS < alex,snore, snore(__), ¬(__) >
Check your answer
¬(snore(alex))
3. PARTS < alex,alex,snore >
Check your answer
There is no possible EX-CONT value because the three elements on the PARTS list cannot be combined.
3. PARTS < alex,alex,snore, snore(__) >
Check your answer
snore(alex)
4. PARTS < alex,alex,snore, snore(__), __ ∧ __ >
Check your answer
snore(alex) ∧ snore(alex)
Analysis of simple sentences
Feel free to send feedback on this exercise to Manfred Sailer.
Basic combinatorics: Canonical examples
(the following exercises are adapted from the textbook material to [Chapter 5].
Possible EX-CONT values
Given the following PARTS lists, what are possible EX-CONT values (if we do not assume other restrictions)
1. PARTS < pat, alex,like, like(__,__) >
Check your answer
like(pat,alex)
like(alex,pat)
2. PARTS < alex,snore, snore(__), ¬(__) >
Check your answer
¬(snore(alex))
3. PARTS < alex,alex,snore >
Check your answer
There is no possible EX-CONT value because the three elements on the PARTS list cannot be combined.
3. PARTS < alex,alex,snore, snore(__) >
Check your answer
snore(alex)
4. PARTS < alex,alex,snore, snore(__), __ ∧ __ >
Check your answer
snore(alex) ∧ snore(alex)
Material for week 13 (23.1.2018)
Material for week 12 (16.1.2018)
Basic syntactic notions
Parts of speech
Feel free to send feedback on this exercise to Manfred Sailer.
Syntactic categories
Feel free to send feedback on this exercise to Manfred Sailer.
Lexical entries as Attribute-Value Matrix
Provide the required information on the lexical properties of the underlined words in the following sentences.
Note:
- Put a minus ("-") if a slot should not receive any filling
- Use det, noun, prep or verb for the HEAD values.
Feel free to send feedback on this exercise to Manfred Sailer.
Material for week 11 (9.1.2018)
Material for week 10 (19.12.2017)
Determiners/quantifiers
Watch the following video on logical determiners:
Exercises
Task 1 Variable assignment function
Start with the following variable assigment function g:
g(u) = Romeo, g(v) = Juliet, g(w) = Romeo, g(x) = Laurence, g(y) = Mercutio, g(z) = Juliet
Provide the changed variable assignment function g[v/Paris].
Check your solutions here:
g[v/Paris](u) = g(u) = Romeo
g[v/Paris](v) = Paris
g[v/Paris](w) = g(w) = Romeo
g[v/Paris](x) = g(x) = Laurence
g[v/Paris](y) = g(y) = Mercutio
g[v/Paris](z) = g(z) = Juliet
After having watched the video, work on the following tasks.
Task 2 Identify the determiners in the following sentence.
(a) Juliet talked to some stranger at the party.
(b) Every Capulet is an enemy to some Montague.
(c) Many people in Verona are not happy about the Capulet-Montague feud.
Check your solutions here:
(a) some
(b) every, some
(c) many
Task 3 Identify the formula that corresponds to the translation of the sentence.
Task 4 The sentence: Some Tybalt loved some Montague. is translated into the formula
∃ y (montague1(y) : love2(tybalt,y)).
Given this table, is the overall formula true or false? (Give a reason for your answer.)
Check your solutions here:
The formula is false, because there is no individual in our model for which both the restrictor and the scope are true.
Material for week 9 (12.12.2017)
Video
Truth tables
Truth tables are also useful to compute the truth value of complex formulae. This is shown in the following podcast, created by Lisa Günthner.
Material for week 6 (21.11.2017)
Video
(Note: the videos contain connectives that we have not talked about in class yet!)
The following video presents the step-by-step computation of the truth value of two formulae with connectives. The example uses a model based on Shakespeare's play Macbeth. The two formulae are:
- ¬ king(lady-macbeth)
- king(duncan) ∨ king(lady-macbeth)
The next video shows how the truth value of a more complex formula can be computed. The example contains two connectives:
kill(malcom,lady-macbeth) ∨ ¬thane(macbeth)
The video shows two different methods: top down and bottom up.
Material for week 5 (14.11.2017)
Video
The following video presents the step-by-step computation of the truth value of two atomic formulae. The example uses a model based on Shakespeare's play Macbeth. The two formulae are:
- kill(macbeth,duncan)
- kill(lady-macbeth,macbet)
Material for week 4 (7.11.2017)
Our literary scenario
Literary scenario: The Fresh Prince of Bel-Air
Wikipedia entry: https://en.wikipedia.org/wiki/The_Fresh_Prince_of_Bel-Air
Why it is too difficult to go directly from language to the world
The following architecture is extremely useful when talking about semantics:
- A natural language expressions: Daenerys loves Drogo.
- ... is mapped to some expression from a formal language (here: predicate logic): love2(daenerys,drogo)
- This logical expression is then interpreted with respect to our scenario/world: The formula love2(daenerys,drogo) is true, because, in our scenario, Daenerys loves Drogo.
The following properties of natural language make it useful to use the intermediate step of a logical language:
- The same expression can have different meanings (ambiguity).
- Different expressions can have the same meaning (synonyms, paraphrases)
Find examples for the above-mentioned properties (ambiguity, synonymy, paraphrases).
Check your answers
1. one form, two meaingns: Ambiguity: (see earlier in this meeting and the slides of last week's meeting)
1.a Ambiguous words: date (fruit or point in time); bank (financial institute or bank of a river)
1.b. Ambiguous sentences: Sycorax and Prospero were stranded on the island with their children.
2. two forms, one meaning:
2.a Synonymous words: couch - sofa; instant - moment
2.b Paraphrases:
- active-passive pairs: Prospero set Ariel free. - Ariel was set free by Prospero.
- cleft sentences: Prospero set Ariel free. - It was Prospero who set Ariel free.
- different ways to express a possessor: Sycorax was the first inhabitant of the island. and Sycorax was the island's first inhabitant.
Towards a formal model
First steps
The following material is an adapted form of material created by student participants of the project e-Learning Resources for Semantics (e-LRS). Involved participants: Lisa, Marthe, Elisabeth, Isabelle.
You can think of building a formal model like being the producer of a film who has to collect everything that should be included in the film.
Here is a very simple story from which we can derive an example model.
The universe and name symbols
Task: Assume three individuals from our Game of Thrones-scenario.
Formally we collect the individuals of our model in a so-called universe (U). For the fairy-tale story, we can define the universe as follows:
U = {Redridinghood, Grandmother, Wolf}
Do a similar definition for your own scenario.
We can introduce name symbols for some of our individuals. For example: redridinghood, grandmother, wolf.
We link the name symbols to the individuals in our modal. To do this, we introduce the interpretation function. We will written the interpretation function as as I.
This function can be defined in the following way:
I(grandmother) = Grandmother
I(redridinghood) = Red Riding Hood
I(wolf) = Wolf
Relations and predicate symbols
In the fairy-tale scenario we express a relation between Little Red Riding Hood and the Wolf, namely that Little Red Riding Hood is the Wolf's afternoon snack. To formalize this, we collect all pairs of individuals which are such that the first element in the pair is the afternoon snack of the second. Note: A pair is written in between pointy brackets.
Formally we can write this down as follows:
{< x, y > | x is y 's afternoon snack} = { < Redridinghood, Wolf >, < Grandmother, Redriding hood >.}
We can also assume empty relations:
{< x, y > | x is y 's father } = { }
Note, if a relation works both ways, two pairs must be added:
{< x, y > | x talks with y} = { <Redridinghood, Wolf >, < Wolf, Redridinghood >}
Just like with names, we want to have symbols that we can use in the logical language. For our example, let's take the predicate symbols afternoon-snack-of_2 and father-of_2, and talks-with_2. (The number 2 indicates that the interpretation consists of pairs, not just of single individual) There interpretation is defined as follows:
I(afternoon-snack-of_2) = { < x, y > | x is y 's afternoon snack } = { <Redridinghood, Wolf >, <Grandmother, Wolf > }.
Task: For each of your properties, invent an appropriate predicate symbol. Define its interpretation.
Properties and predicate symbols
A property is a specification that either holds of an individual or not. In the little story, having a big mouth is a property of the Wolf, but of noone else in the story. Being female holds of both Little Red Riding Hood and the Grandmother.
We can think of a property as the set of individuals that have this property. Under this view, the property of being female would be the set {Redridinghood, Grandmother}.
Alternatively it is convenient to think of properties as 1-place relations. Under this view, the property of being female would be a set of lists of length 1. This is what the property of being female then looks like: { <Redridinghood>, <Grandmother> }
Task: Using your Game of Thrones universe, define two properties in the format of 1-place relations.
Just like before, we want to have symbols that we can use in the logical language. For our example, let's take the predicate symbols female_1 and has-big-mouth_1. There interpretation is defined as follows:
I(female_1) = { < x > | x is female } = { <Redridinghood>, <Grandmother> }.
Task: For each of your properties, invent an appropriate predicate symbol. Define its interpretation.
Computing the truth value of atomic formulae
The following video presents the step-by-step computation of the truth value of two atomic formulae. The example uses a model based on Shakespeare's play Macbeth. The two formulae are:
- kill(macbeth,duncan)
- kill(lady-macbeth,macbeth)
Back to the course page.